Leetcode E2215 Find the Difference of Two Arrays, M1456 Maximum Number of Vowels in a Substring of Given Length, E1572 Matrix Diagonal Sum Optimization

E2215 description:
  Given two 0-indexed integer arrays nums1 and nums2, return a list answer of size 2 where:
    answer[0] is a list of all distinct integers in nums1 which are not present in nums2.
    answer[1] is a list of all distinct integers in nums2 which are not present in nums1.
  Note that the integers in the lists may be returned in any order.
Constraints:
  1 <= nums1.length, nums2.length <= 1000
  -1000 <= nums1[i], nums2[i] <= 1000

Almost all the solutions use two tables, but actually one table is enough.

Code

char tab_b[2001];
char* tab=tab_b+1000;
class Solution {
public:
    vector<vector<int>> findDifference(vector<int>& nums1, vector<int>& nums2) {
        memset(tab_b,0,sizeof(tab_b));
        for(int n:nums1){
            tab[n]=1;
        }
        vector<int> r1,r2;
        r1.reserve(nums1.size());
        r2.reserve(nums2.size());
        for(int n:nums2){
            if(tab[n]==0){
                if(tab[n]!=2) r2.emplace_back(n);
            }
            tab[n]=2;
        }
        for(int n:nums1){
            if(tab[n]==1){r1.emplace_back(n); tab[n]=0;}
        }
        return vector<vector<int>>{r1,r2};
    }
};

Runtime 7 ms Beats 100%
Memory 26.7 MB Beats 94.43%

---

M1456 description:
  Given a string s and an integer k, return the maximum number of vowel letters in any substring of s with length k.
  Vowel letters in English are 'a', 'e', 'i', 'o', and 'u'.
Constraints:
  1 <= s.length <= $10^5$
  s consists of lowercase English letters.
  1 <= k <= s.length

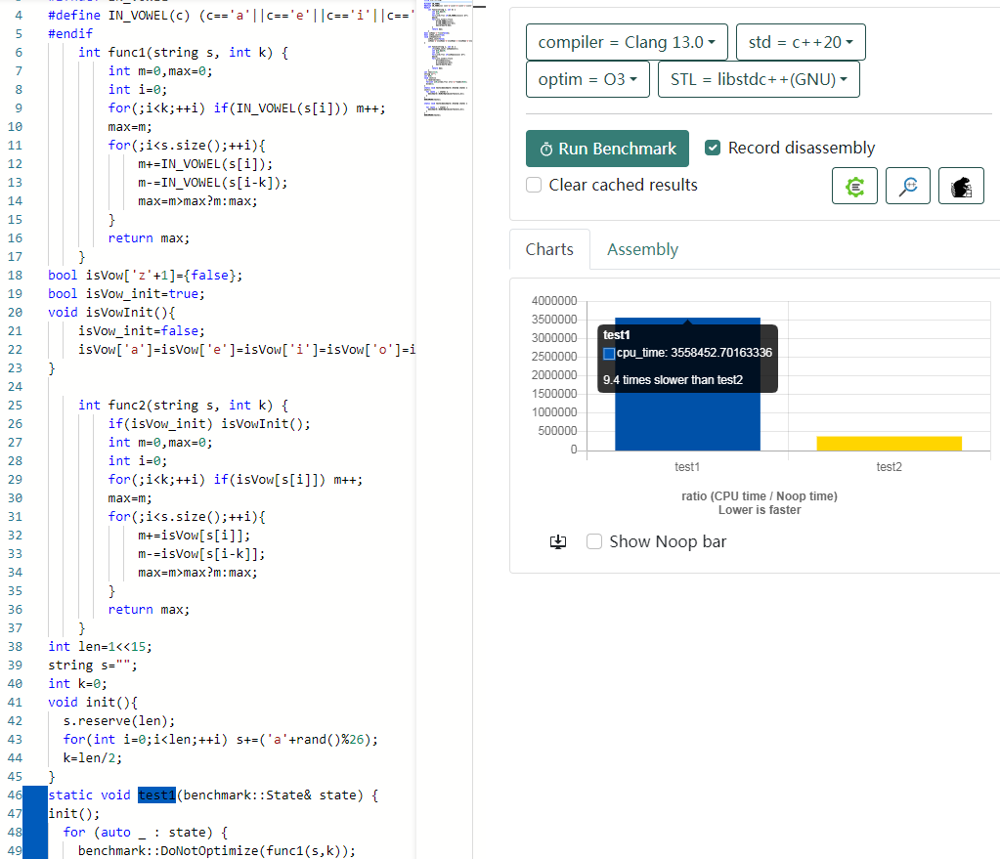
Another very easy problem. But is your solution optimized? The following method may be 10 times faster:

Code

class Solution {
    bool isVow['z'+1]={false};
    void isVowInit(){
        isVow['a']=isVow['e']=isVow['i']=isVow['o']=isVow['u']=true;
    }
public:
    Solution(){
        isVowInit();
    }
    int maxVowels(string s, int k) {
        int m=0,i=0;
        for(;i<k;++i) if(isVow[s[i]]) m++;
        int max=m;
        for(;i<s.size();++i){
            m+=isVow[s[i]];
            m-=isVow[s[i-k]];
            max=m>max?m:max;
        }
        return max;
    }
};

1 operation instead of (mostly and at most) 5, so I was expecting a 5x speedup. But somehow it’s almost 10 times faster?

---

E1572 description:
  Given a square matrix mat, return the sum of the matrix diagonals.
  Only include the sum of all the elements on the primary diagonal and all the elements on the secondary diagonal that are not part of the primary diagonal.

Also very easy. But instead of checking if we are at the center every time, we can just check it once at the end. Also we can do it in one iterations instead of 2.

class Solution {
public:
    int diagonalSum(const vector<vector<int>>& mat) {
        int s=0;
        const int l=mat.size();
        for(int i=0;i<l;++i) s+=mat[i][i]+mat[l-1-i][i];
        return s-l%2*mat[l/2][l/2];
    }
};