I thought this function was helpful for solving another problem. It did work, but it was unnecessary since there were faster algorithms to solve it. But I was interested, so I ended up finishing it. The algorithm iterates through all possible ways to match $2n$ points, i.e. chord diagrams.

Input constraints: $v.size()$ is even, elements are distinct and comparable, $v[2i]<v[2i+1]$.
Complexity: $O(n)$ 

template<typename T>
bool next_matching(vector<T>& v){
    if(v.size()<=2) {return false;}
    size_t s=v.size();
    int mini=v[s-2],maxi=v[s-1];
    size_t start=s-4;
    while(start>0&&v[start]<=v[start+2]&&v[start+1]>=v[start+3]){start-=2;mini=v[start];maxi=v[start+1];}
    if(start==0&&v[0]<=v[2]&&v[1]>=v[3]){
        vector<T> v1(s);
        for(size_t i=0;i<s/2;++i){v1[i]=v[2*i];v1[s-i-1]=v[2*i+1];}
        v=move(v1);
        return false;
    }
    vector<int> v1(s);
    for(size_t i=0;i<=start+1;++i){
        v1[i]=v[i];
    }
    for(size_t i=0;i<(s-start)/2-1;++i){
        v1[start+2+i]=v[start+2+2*i];v1[s-i-1]=v[start+2+2*i+1];
    }
    size_t u=upper_bound(v1.begin()+start+2,v1.end(),v1[start+1])-v1.begin();
    swap(v1[start+1],v1[u]);
    v=move(v1);
    return true;
}

Sample output: 

vector<vector<int>> allMatchings(int n){
    vector<int> v(n);
    for(int i=0;i<n;++i) v[i]=i;
    int cnt=1;
    for(int i=n-1;i>0;i-=2) cnt*=i;
    vector<vector<int>> r;
    r.reserve(cnt);
    r.emplace_back(v);
    while(next_matching(v)) r.emplace_back(v);
    return r;
}
int main(){
    vector<vector<int>> r=allMatching(6);
    for(auto&v:r){
        for(int i=0;i<v.size()/2;++i){
            cout<<"("<<v[2*i]<<","<<v[2*i+1]<<")";
        }
        cout<<endl;
    }
    return 0;
}

output:
(0,1)(2,3)(4,5)
(0,1)(2,4)(3,5)
(0,1)(2,5)(3,4)
(0,2)(1,3)(4,5)
(0,2)(1,4)(3,5)
(0,2)(1,5)(3,4)
(0,3)(1,2)(4,5)
(0,3)(1,4)(2,5)
(0,3)(1,5)(2,4)
(0,4)(1,2)(3,5)
(0,4)(1,3)(2,5)
(0,4)(1,5)(2,3)
(0,5)(1,2)(3,4)
(0,5)(1,3)(2,4)
(0,5)(1,4)(2,3)

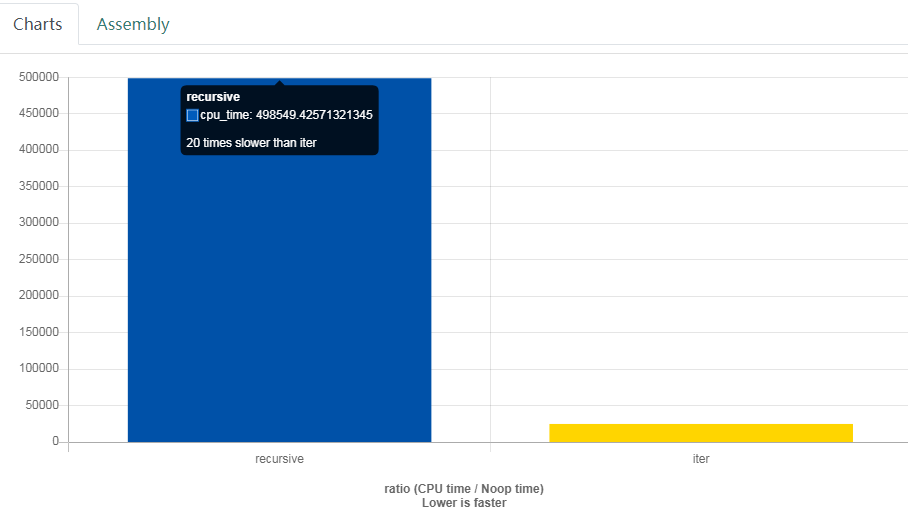
The only other place that mentions the same problem is here, solved with a recursive algorithm. But the iterative is more efficient. Benchmarking shows that the recursive solution is 20 times slower for input size $2n=8$, and 30 times slower for input size $2n=10$.

Benchmarking result

Not sure what the applications might be, but I'll just share it here.